Up

「かけ算の順序」は現行では主題にできない

---

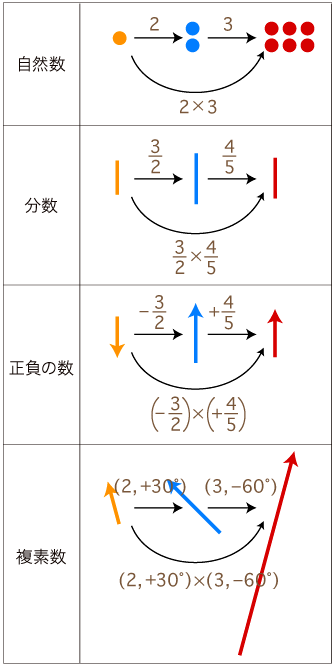
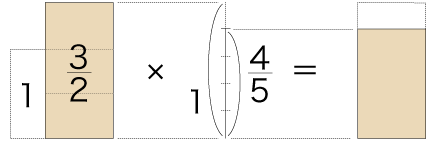
ここまで，「順序」はつねに重要であると論じ，「かけ算の順序」の学習が教員に必要であると論じた。 しかしこの論を無しにするような言い方になるが，現行では，「かけ算の順序」は指導主題にならない。 なぜなら，学校数学の「かけ算」が，＜数は量の抽象＞が謂う「かけ算」であり，「かけ算の順序」の一貫した論理・形式──すなわち，「×」の文法──を扱えないからである。 実際，「×」の文法はつぎのようであり，「かけ算の順序」の意味はこの「×」の文法に示されていることがすべてである： これに対し，＜数は量の抽象＞の謂う「かけ算」は，つぎのような錯綜した図をいわば＜気持＞で飲み込んでいくというものになる： そして＜気持＞で飲み込めるのも分数までであり，正負の数，複素数では無理となる。 実際，＜数は量の抽象＞は，小学算数で閉じていることで──小学算数の先を見ないで済ますことで──保っている。 そしてこのことがまた，小学算数を学校数学の中でますます特異なものにしていくのである。(「算数は数学とは違うのだ！」の気分醸成)