Up 各様モンスターが論点を攪乱 作成: 2012-01-12
更新: 2012-01-20

    「かけ算の順序」論争は，つぎの２つの思考回路の間の論争である：
    1. 遠山の「１あたり量 × いくつ分」を自分の立場とする遠山主義
    2. 「１あたり量 × いくつ分 は，なぜこの順序でなくてはならないのか？」から「かけ算に順序はない」に短絡するモンスター
    そしてこの基本構図に，＜論点の攪乱＞といった格好で，各様モンスターが彩りをつけていく。
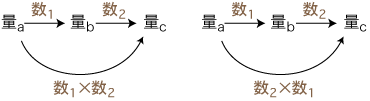
    例として，ここでは特に目立つ二つのタイプのモンスターを，以下に示す。


    (1)「いくつ分 × １あたり量 の順序もあり」の理屈がモンスター

    例えば，言語相対論を持ち出してくるモンスター：
      作用の記述「Ａに，Ｂを作用させる」は，別の言語では「Ｂを作用させる，Ａに」の並びになる。
      かけ算の順序は，これと事情が同じだ。
      だから，かけ算に順序はない。

    このモンスターの所以は，つぎの２つ (定義と推論) の区別を知らない，あるいは区別できないことである：
    1. 記号「×」の定義──つぎのどちらを「×」の文法として採用するか：


    2. 推論が積の式を導く

    記号「×」をはさむ２数の順序が任意になるのは，Aの場面である。 この場面だと，順序の＜取り決め＞の恣意性を議論することが意味をもち，言語相対論にも出る幕がある。
    しかし，「×」の文法をいったん取り決めたら，以降，この取り決めを遵守することになる。 ──数学とはこういうものである。
    そして，推論が積の式への還元であるとき，「×」をはさむ２数の順序は一意に定まる。
    　( 問題の論理的還元──例 :「3×2」の立式の場合 )


    (2)「こだわるべきではない」のことばの使い方がモンスター

    「かけ算の順序」論争が論争であるならば，それはかけ算の順序が＜ある＞と＜ない＞の間の論争である。 しかし現前の論争は，＜ある・ない＞をきちんと言い切るということがない。
    ＜ある・ない＞をきちんと言い切るとは一つの理論を示すことであるが，理論レベルで＜ある・ない＞を主張しているわけではないので，こうなるのである。

    そこで，どんなもの言いになるか？
    「順序にこだわるべきではない」のもの言いになるのである。

    「こだわる」は，この「かけ算の順序」論争の場合だと，本来つぎのように使うことばである：
    「かけ算の順序は＜ある＞と＜ない＞のどちらが正しいのか？に，こだわりをもつ。」
    「正しいのはこの立場であるが，この立場が択られるかどうかについてはこだわらない。」
    そして，このときの「正しい」は，数学の上で決着される「正しい」である。

    しかし，「かけ算の順序」論争には，数学がない。
    数学をもっていないので，順序の＜ある・ない＞が言えない。
    そこで，「こだわるべきではない」を，便利な言い回しとして使う。
    そして，このことばの用い方がおかしいことに，自分では気づかないのである。