長方形は,「タテの長さa,ヨコの長さbの長方形」の見方をすることで,長さの対 (a,b) に表現できる。 そこで,長さ全体の集合をQとして,積集合 Q×Q を長方形全体の集合の表現とすることができる。 ここで × の前後のQを区別するために,それぞれタテ,ヨコで表すとしよう。 タテ×ヨコ の要素 (a,b) を「タテの長さa,ヨコの長さbの長方形」と読もうというわけである。 ここで「面積」の対象化ということを考える。 面積を一つ定めるとは,どういうことか?何をすることか? 答えは,「タテの長さa,ヨコの長さbの長方形の面積」のように,《面積を「の」つきで定義する》である。 「なになにの面積」というふうに面積を対象化するのである。 実際,循環論法をやるのでなかったら,これの他にどんな方法があるか? これの他にはない。 ところで,面積を<長方形の面積>で定義しようという場合,この定義は一つの面積を一つの長方形で定義するというふうにはならない。 すなわち,《異なる長方形が同じ面積を定める》の考慮が要る。 そこで,「面積が同じ長方形のグループの,その面積」というふうに面積を定義することになる。 これをどうやるか? 面積を定義するのに「面積が同じ長方形のグループ」のことばをそのまま使ったら,循環論法になる。 答えは,「面積が同じ長方形のグループ」をつぎのように言い替えることである:
この類を要素にする集合──すなわち,商集合──を,ここでは タテ 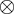 ヨコ で表す。 ヨコ で表す。
この集合の要素は (a, b) ∈タテ×ヨコ に対する「(a, b) の属する同値類」と表現されるものになるが,このときの「(a, b) の属する同値類」の意味は「タテの長さa,ヨコの長さbの長方形と同じ面積の長方形全体」である。 「(a, b) の属する同値類」を,a  bで表す。
もしグループ「タテの長さa,ヨコの長さbの長方形と同じ面積の長方形全体」にタテの長さa',ヨコの長さb' の長方形が属していれば, a bで表す。
もしグループ「タテの長さa,ヨコの長さbの長方形と同じ面積の長方形全体」にタテの長さa',ヨコの長さb' の長方形が属していれば, a b = a' b = a' b' となる。 b' となる。
以上は,面積の対象化 (対象構築) の話である。 ここで,「面積の対象化」の話は横において,面積を所与にする。 特に,長さと同型な量として面積を所与にする:
( (面積, +), ×, (数, +, ×) ) §「2個/皿 × 3皿 = 6個」の計算) この面積は,つぎを含意するものになっている:

can: (a, b)├─→ a  b b
導入が長くなったが,この可換図式の一般論が「テンソル積」である。 テンソル積の定義は,複比例関数F:Q1 × Q2 → Q3 から出発する。 Fの値が同じになる Q1 × Q2 の要素を同じ類にして,この類の集合をQ1 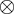 Q2 で表す。 Q2 で表す。
また,この集合の要素で, (a,b) ∈ Q1 × Q2 の属する類になるものを,a  b で表す。 b で表す。
このとき,つぎの可換図式が成り立つ: 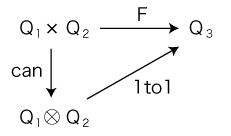
can: (a, b)├─→ a  b b
|