Up 「標本調査」の授業の構成──論理的構成 作成: 2014-06-17
更新: 2014-06-18

    「標本調査」の授業構成は，＜論理的構成＞ということであれば，いろいろにはならない。自ずと定まる。
    即ち，主題が「標本調査」なのであるから，つぎのような流れになる：

    1. 「大豆の製品袋からｎ個を無作為抽出し，重さを測定し，母平均を推定する。
      　これが課題である。      」

    2. 「階級を適切に設定して，標本度数分布をヒストグラムに表せ。
      　標本平均を求めよ。
      　標本標準偏差を求めよ。
      　母平均の 95%の信頼区間を求めよ。      」

    3. 「今度は，標本の大きさをｎ個よりずっと大きくして，同様のことをせよ。
      　標本標準偏差は，どうなったか。
      　母平均の 95%の信頼区間は，どうなったか。      」

    4. 「標本が大きいほど信頼度は増すが，計算の手間も増す。
      　両者のトレードオフを考えよ。      」


    1, 2 では，つぎのようになる。
    ──簡単のために，階級３つにする。

    1. 標本の大きさ ｎ＝10
      つぎの場合：

      これの平均ｍは，

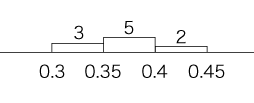
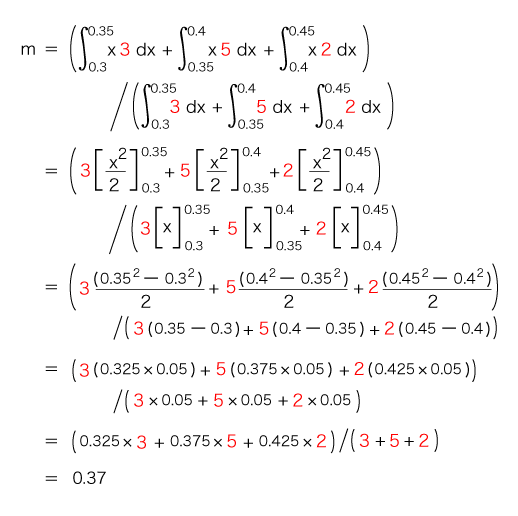
      分散ｓ2 は，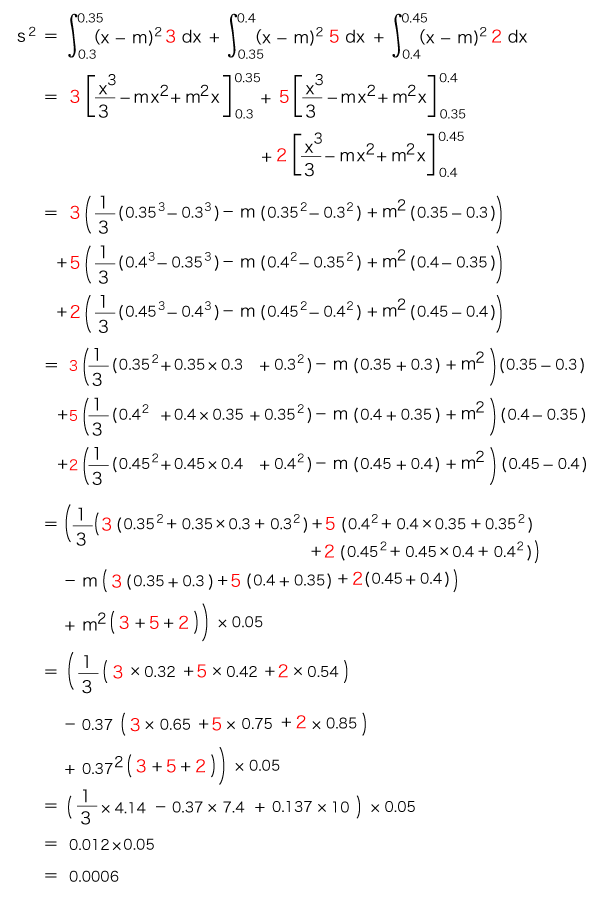

        （標本がそもそも小さいので，分散の値も小さくなる）

      標準偏差ｓは，
        ｓ＝ √0.0006 ＝ 0.024

      母平均μの信頼度 95% の信頼区間は，母標準偏差σで，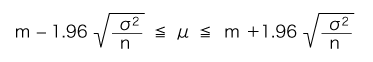
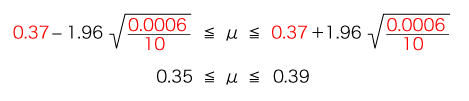
      そこで，ｓを母標準偏差σと見なした場合，

    2. 標本の大きさ ｎ＝100
      上の標本の単純10回累加の場合：

      これの平均ｍは，

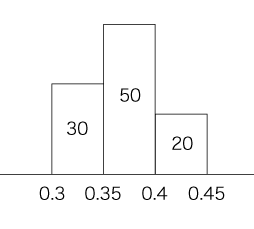
        （平均は，理屈からして，１と同じ）

      分散ｓ2 は，

      標準偏差ｓは，
        ｓ＝ √0.0006 ＝ 0.078

      ｎ＝100 であれば ｓは母標準偏差σに見なせるとして，母平均μの信頼度 95% の信頼区間は，

    3. 標本の大きさ ｎ＝100
      つぎの場合：

      これの平均ｍは，

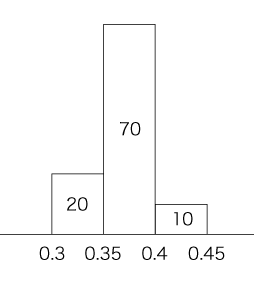
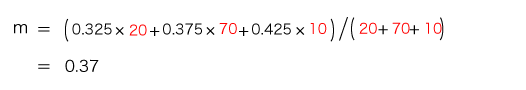
      分散ｓ2 は，

      標準偏差ｓは，
        ｓ＝ 0.05

      ｎ＝100 であれば ｓは母標準偏差σに見なせるとして，母平均μの信頼度 95% の信頼区間は，

        （信頼区間の幅が，２より狭まった）


    比較として，上のヒストグラム (連続型) を，柱の中央値に度数をのせた格好の棒グラフ (離散型) に替え，このときの計算がどうなるかを見てみる。

    1. 標本の大きさ 10個
      つぎの場合：

      これの平均ｍは，
        ｍ＝（ 0.325 × 3 ＋ 0.375 × 5 ＋ 0.425 × 2 ) / ( 3 ＋ 5 ＋ 2 )
        　　＝ 0.37
      分散ｓ2 は，
        ｓ2 ＝（ 0.325 - 0.37 )2 × 3
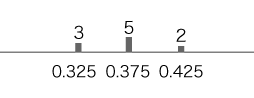
        　　＋ ( 0.375 - 0.37 )2 × 5
        　　＋ ( 0.425 - 0.37 )2 × 2
        　　＝ 0.0452 × 3 ＋ 0.0052 × 5 ＋ 0.0552 × 2
        　　＝ 0.002025 × 3 ＋ 0.000025 × 5 ＋ 0.003025 × 2
        　　＝ 0.01225
        （標本がそもそも小さいので，分散の値も小さくなる）

      標準偏差ｓは，
        ｓ＝ √0.01225 ＝ 0.11

    2. 標本の大きさ 100個
      上の標本の単純10回累加の場合：

      これの平均ｍは，
        ｍ＝（ 0.325 × 30 ＋ 0.375 × 50 ＋ 0.425 × 20 ) / ( 30 ＋ 50 ＋ 20 )
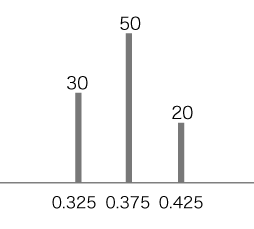
        　　＝ 0.37
        （平均は，理屈からして，１と同じ）

      分散ｓ2 は，
        ｓ2 0.002025 × 30 ＋ 0.000025 × 50 ＋ 0.003025 × 20
        　　＝ 0.1225

      標準偏差ｓは，
        ｓ＝ √0.1225 ＝ 0.35

    3. 標本の大きさ 100個
      つぎの場合：

      これの平均ｍは，
        ｍ＝（ 0.325 × 20 ＋ 0.375 × 70 ＋ 0.425 × 10 ) / ( 20 ＋ 70 ＋ 10 )
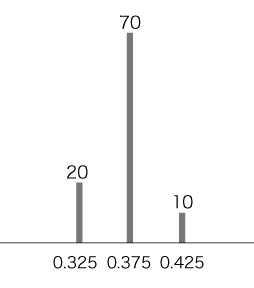
        　　＝ 0.37

      分散ｓ2 は，
        ｓ2 ＝ 0.002025 × 20 ＋ 0.000025 × 70 ＋ 0.003025 × 10
        　　＝ 0.0725
        （分散が，2より小さくなった）

      標準偏差ｓは，
        ｓ＝ √0.0725＝ 0.27