言語は,この方法を既に与えている。 「花」ということばは,「違うけれども<花>として同じに見る」よう仕向ける。 教科は,「違うものを同じに見る」のうち重要なものを,分担して主題化する。 この場合の「同じ」の意味は,「形/構造が同じ」──「同形/同型」──である。
数学は,「形/構造」「同形/同型」を明示的に主題化する学問である。 数学は,「形/構造」「同形/同型」の記述を開発してきた。
数学の「同形/同型」は,定義がシンプルである分だけ,ひどくラディカルになる。 すなわち,とんでもなく違って見えるものが同じになり,またその逆に,同じに見えるものが違うものになってしまう。 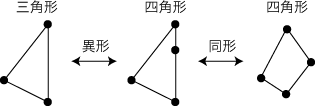 このシンプルとラディカルが,「形/構造」「同形/同型」をとらえ・考える能力を鍛え,「形/構造」「同形/同型」にこだわるカラダの構えを鍛える。 |