「場」の力学では,「エネルギー」の意味は「場を生成するもの」である。
いま,一個のエネルギーA が場所 \( \vec{a} \) に有ることで生成される力ベクトルの場 \( \vec{F}(\vec{x}) \) を考える。
このとき「場」の力学は, つぎの「逆2乗法則」を措く:
\[ \vec{F}(\vec{x}) \,=\, - \frac{1}{|\vec{x} - \vec{a}|^2} \vec{e}_{\vec{x} - \vec{a}}
\ \left( \,=\, \frac{1}{|\vec{x} - \vec{a}|^2} \vec{e}_{\vec{a} - \vec{x}} \right)
\]
ここで,\(\vec{e}_{\vec{x} - \vec{a}} \) は,\( \vec{x} - \vec{a} \) と同方向の単位ベクトル:
\[ \vec{e}_{\vec{x} - \vec{a}} \,=\, \frac{\vec{x} - \vec{a}}{|\vec{x} - \vec{a}|} \]
このとき,つぎを「ポテンシャル」として立てることができる:
(1)「引力」モデル
\[ \phi(\vec{x}) \,=\, - \frac{1}{|\vec{x} - \vec{a}|} \]
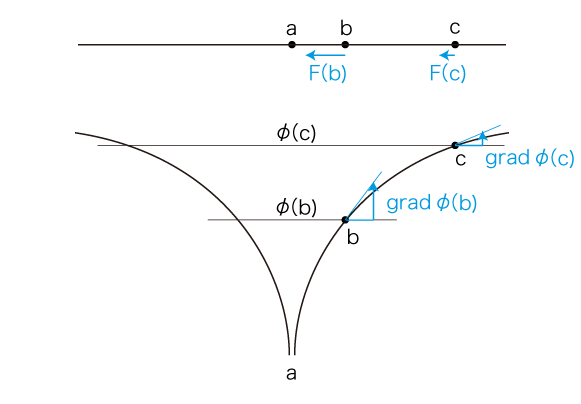
(2)「斥力」モデル
\[ \phi(\vec{x}) \,=\, \frac{1}{|\vec{x} - \vec{a}|} \]
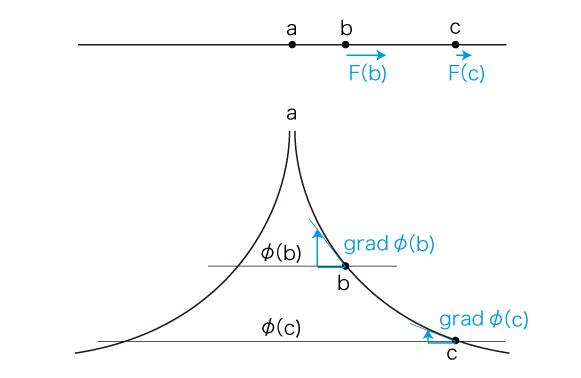
実際,両方のモデルで,「ポテンシャル」の導入の要件となるつぎの条件が満たされている:
(1) \( rot \,\vec{F}(\vec{x}) \,=\, 0 \)
(2) \( grad \,\phi(\vec{x}) \,= \, - \vec{F}(\vec{x}) \)
引力モデルと斥力モデルでは,\( \phi(\vec{x}),\, \vec{F}(\vec{x}) \) の定義式が違ってくる。
即ち,引力モデルの式と斥力モデルの式は,符合が逆である。
しかしこのことに神経質になる必要はない。
ここでの肝心要は,\( \phi(\vec{x}) \) と \( \vec{F}(\vec{x}) \) が同符号になっていることである:
\( \phi(\vec{x}) \) の grad をとると,符合が逆になる。
そして,\( grad\,\phi(\vec{x}) \) の符合を逆にしたのが \( \vec{F}(\vec{x}) \) だから,\( \phi(\vec{x}) \) と \( \vec{F}(\vec{x}) \) は同符号になる。
よって,どんなモデルであれ,それがモデルであるためには,\( \phi(\vec{x}) \) と \( \vec{F}(\vec{x}) \) が同符号になっていなければならない。
「\( grad \,\phi(\vec{x}) \,= \, - \vec{F}(\vec{x}) \)」の証明 (引力モデル):
\[
grad \,\phi(\vec{x}) \\
\,=\, \left( \frac{\partial}{\partial x} \frac{-1}{|\vec{x}-\vec{a}|} ,\,
\frac{\partial}{\partial y} \frac{-1}{|\vec{x}-\vec{a}|} ,\,
\frac{\partial}{\partial y} \frac{-1}{|\vec{x}-\vec{a}|} \right) \\
\ \\
\frac{\partial}{\partial x} \frac{-1}{|\vec{x}-\vec{a}|} \\
\,=\, \frac{\partial}{\partial x} \frac{-1}{( (x-a_x)^2 + (y-a_y)^2 + (z-a_z)^2)^{\frac{1}{2}} } \\
\,=\, (-1)(-\frac{1}{2}){( (x-a_x)^2 + (y-a_y)^2 + (z-a_z)^2)^{-\frac{3}{2}} } (2 (x-a_x)) \\
\,=\, \frac{1}{|\vec{x}-\vec{a}|^2} \frac{x-a}{|\vec{x}-\vec{a}|}
\]
よって,
\[
grad \,\phi(\vec{x}) \\
\,=\, \left(
\frac{1}{|\vec{x}-\vec{a}|^2} \frac{x-a_x}{|\vec{x}-\vec{a}|} ,\,
\frac{1}{|\vec{x}-\vec{a}|^2} \frac{y-a_y}{|\vec{x}-\vec{a}|} ,\,
\frac{1}{|\vec{x}-\vec{a}|^2} \frac{z-a_z}{|\vec{x}-\vec{a}|} \right) \\
\,=\, \frac{1}{|\vec{x} - \vec{a}|^2} \vec{e}_{\vec{x} - \vec{a}} \\
\,=\, - \vec{F}(\vec{x})
\]
|

