Up 波動 作成: 2020-01-07
更新: 2020-01-07

    前進する大群衆の先に，壁が待ち構えている。
    その壁に，幅10メートルの通り口がある。
    直進のままこれを通れる者は，これを通って壁の向こう側に進む。

    このとき，壁の向こう側の人の流れは，つぎのようになる：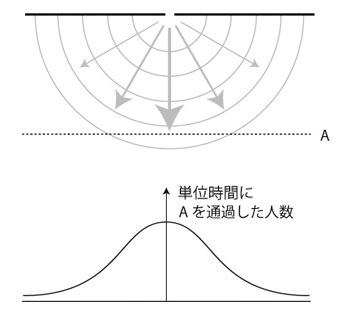

    つぎに，通り口が二つあったとする。
    このときの人の流れはどうなるか？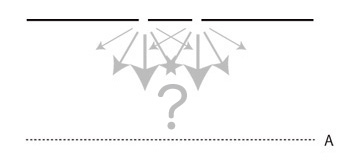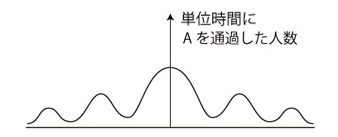
    二つの通路から出た二つの流れが干渉し合い，つぎのようになる：

    これは，ほんとうの話ではない。
    これは，アナロジー/パロディーである。
    アナロジー/パロディーのもとは，光子を対象にした「ヤングの実験」および電子を対象にした「トムソンとデイヴィソンの実験」である。

    この話の趣旨は，《群集の運動の捉えは，「波動」の見方がうまくいくかも知れない》である。
    このとき，個の分布の粗密パターンに，波形が対応する。──粗は波の「低い」ところ，密は「高い」ところ。
    また，同じ粗密パターンでも濃さの違いを考えることができるが，これには波の振動数/波長が対応する。

    なお，「波動」とは，《個が近接の個の動きに連動する》のダイナミクスが現すものを謂う。
    上の例では，壁の向こうの群集の形が定常だが，それは《個が近接の個の動きに連動する》のダイナミクスが現しているものであり，波動である。