実際,「接平面・地図」の概念の導入は,「曲がった空間」を定立するためである。 一般相対性理論は,われわれの空間を「曲がった空間」として主題化しようとする。 ──ここで「空間を曲げるもの」の身分を与えられるのが,「重力」である。 こうして,一般相対性理論がわれわれの空間を主題化する形は,「多様体」である。 しかし,われわれの空間を「多様体」に見なすとは,どんなふうにすることか? ひとはここで,<わかったつもり>になろうとする。 <わかったつもり>は,低次元の喩えに寄り掛かることで得ている:
「1次元人──1次元多様体に棲む」
「2次元人」の喩えで使う多様体絵は,球面である: 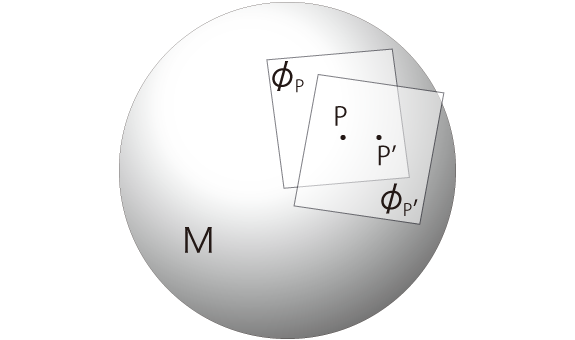
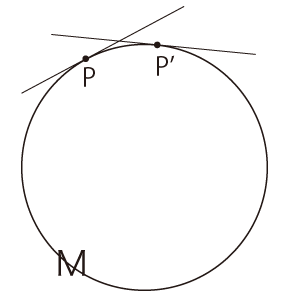
この絵を,低次元の延長として,飲み込むというわけである。 しかしこれは,<飲み込んだつもり>である。 実際,この絵図をどう使えるというのか。 多様体の絵は,接平面・接線のシフト──「接ベクトル空間のシフト」──が要点になる。 上の絵は,実 real 空間の表面を接ベクトル空間がスライドするような絵になっている。 接ベクトル空間の「シフト」を,「スライド」にしているわけである この絵は,「3次元人」へは延長できない。 次元の延長は,単純なものではないのである。 実際,次元の延長は,多様体の絵をすっかり変えるものになる。 3次元超球面上での接ベクトル空間 (3次元) のシフトは,どんな絵図を以て理解されるものになるか。 シフトの絵の要点は,シフトの方向である。 即ち,シフトが進行する軸である。 これを時間軸に定めると,『相対性理論』になる。 時間のシフトを,「接ベクトル空間のシフト」と定めるのである:
この解釈は,現実的かつ有効・有益なソルーションである。 実際,他にどんな解釈を立てられるというのか。 この解釈は,「実際 practical 存在の多重化」になっている。 さらに言えば,\( M \) に<実 real 存在>を措き,接ベクトル空間に<実際 practical 存在>を措く形の存在論になっている。 存在論の類型としては,プラトニズムということになる。 こうして,多様体の絵図はつぎのようになる: 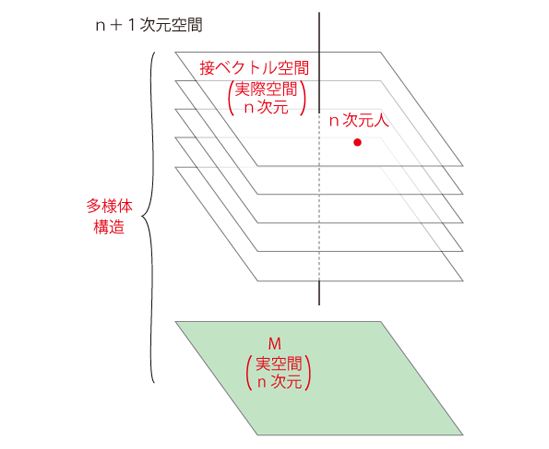
これに応じて「2次元人」「1次元人」の絵図も,つぎのようになる: 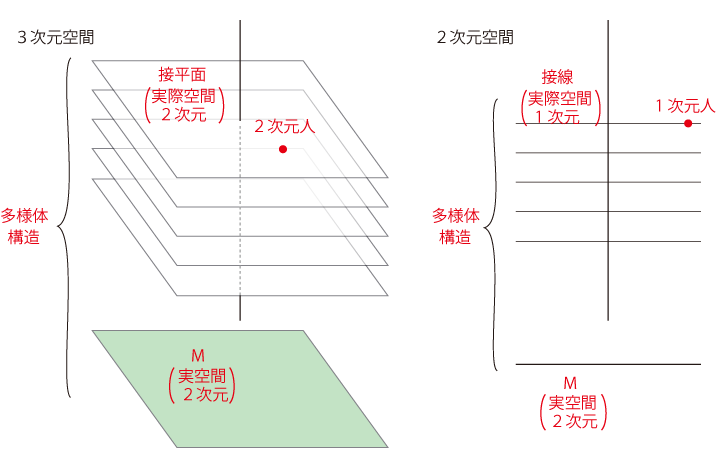
この多様体は,絵が「接平面の束」になるものである。 1次元多様体・2次元多様体を3次元に延長しようとすると,このように1次元多様体・2次元多様体の方が,その解釈を変えられることになる。 この構造の数学名称は,「ファイバーバンドル」である。 接平面を「ファイバー」とする「束 bundle」が,多様体である。 多様体 \(M\) の「点」は,縦軸の点 \(t\) と, \(t\) に対応する接平面 \(T_t\) の点 \(w\) の組 \( (t,\,w)\) である。 そして \( (t,\,w)\) に対応する地図 \(\phi_{t,w} \) は,\( (t,\,w)\) の\(T_t\) における近傍 \(U_{t,w}\) の地図である。 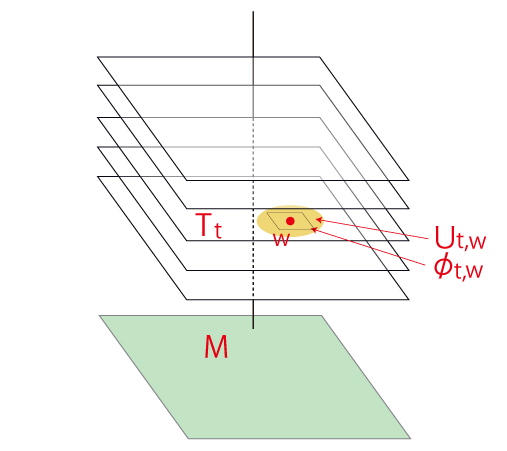
|