2点A, B間の距離は,ベクトル \( \vec{AB} \) の大きさ (長さ) として定義される。
ベクトル \( \bf a \) の大きさ \( | \bf{a} | \) は,内積 \( \bf{a} \cdot \bf{a} \) の平方根で定義される。
そこで,内積が4元化されれば,距離が4元化されることになる。
内積の4元化は,つぎのようにして成る:
- つぎの行列を導入する:
\[
\eta = ( \eta_{ij} ) =
\left(
\begin{array}{cccc}
-1 & & & \\
& 1 & & \\
& & 1 & \\
& & & 1 \\
\end{array}
\right)
\]
- ベクトル \( \bf{a} \,,\, \bf{b} \) の内積 \( \bf{a} \cdot \bf{b} \) を,任意の慣性系Sでのそれぞれの座標 \( \left( a^0, a^1, a^2, a^3 \right) \,,\, \left(b^0, b^1, b^2, b^3 \right) \) によるつぎの行列の積で,定義する:
\[
{}^t \left(a^i \right) \left(\eta_{ij} \right) \left(b^i \right) \\
\left( \,= \left( \eta_{ij} a^i b^j \right)\, = - a^0 b^0 + a^1 b^1 + a^2 b^2 + a^3 b^3 \right)
\]
実際,\( {}^t (a^i)\ (\eta_{ij})\ (b^i) \) の値は慣性系Sのとり方に依らない──ローレンツ変換 \( \Lambda \) に対して不変──である:
\( {a^{'}}^i = {{\Lambda}^i}_j a^j \,,\, {b^{'}}^i = {{\Lambda}^i}_j b^j \) のとき,つぎが成り立つ:
\[
{}^t \left({a^{'}}^i \right) \left(\eta_{ij} \right) \left({b^{'}}^i \right) \,=\, {}^t \left( a^i \right) \left( \eta_{ij} \right) \left( b^i \right) \\
(\ - {a^{'}}^0 {b^{'}}^0 + {a^{'}}^1 {b^{'}}^1 + {a^{'}}^2 {b^{'}}^2 + {a^{'}}^3 {b^{'}}^3 \\
\ \ \ \,=\, - a^0 b^0 + a^1 b^1 + a^2 b^2 + a^3 b^3\ )
\]
以上のように定義された「内積」──4元内積と呼ぶことにする──は,ニュートン力学の中の内積の拡張になっている。
実際,3次元空間は,4次元時空間 (ミンコフスキー空間) の「現在」超平面として埋め込まれることになる:
Wikipedia (「ミンコフスキー空間」) より引用
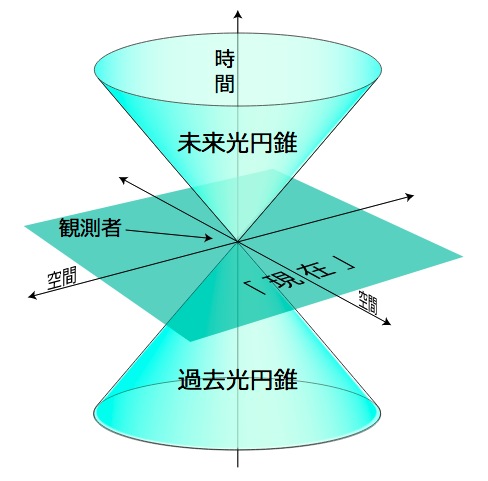
そしてこの超平面は,点の座標の ct 成分が0になるところであり,よって4元内積がニュートン力学の内積と同値になるところである。
|
