他の任意の慣性系S′ から見ても同じくTであるようにする》 世界線wとその上の2点A, Bに対し,慣性系Sを任意にとって,つぎの積分を立てる:
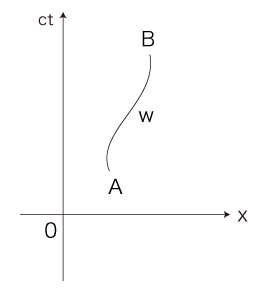
そこでこれを,「wに沿ったAからBの固有時間」と定義する。 このように定義した固有時間は,実際,静止した時計Cが表す時間と一致する: \[ \int_A^{B} \sqrt{ 1 - \frac{ | 0 |^2}{c^2} } \,dt \,=\, \int_0^{T} \sqrt{ 1 - \frac{ | 0 |^2}{c^2} } \,dt \,=\, T \] 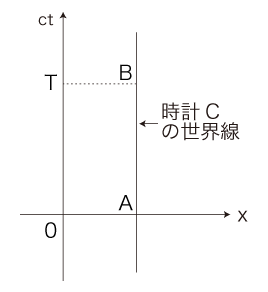
|