白玉赤玉をそれぞれ多数,箱に入れる。
そして箱を振る。
降り続けていると,白赤が均等に混じった状態に至り,その後偏った分布に戻るということは無い。
このことは,「均等な分布の確率は高く,偏った分布の確率は低い」で説明される。
では,どうして「均等な分布の確率は高く,偏った分布の確率は低い」のか?
これは「場合の数」で説明される。
「場合の数」とは:
<分布 \( A \) になる球の配置>の数 \( n(A) \)
\( A \) が均等な分布のとき \( n(A) \) は大きく,\( A \) が偏った分布のとき \( n(A) \) は小さい。
これが,「均等な分布の確率は高く,偏った分布の確率は低い」の中身である。
「場合の数」は,「要素の組み合わせの数」として計算される。
ここでの白玉赤玉の例だと,分布 \( A \) になる球の配置を,球の組み合わせに表現して,組み合わせの数を計算する。
計算では,条件をいろいろ設定することになる。
特に,「偏り」をどう表現するかが,考えどころになる。
簡単な表現を用いれば,計算が簡単になる。
──「簡単な表現」とは,若干の非現実的・曖昧な点は目をつぶるということである。
赤玉白玉の個数を,同数の \( N \) とする。
そして,箱の中の白玉赤玉の偏りを,
で表現する。
偏りの最大は \( n \) が 0 と \( N \) のとき,そして偏りの最小 (均質) は \( N/2 \) のとき,というわけである。
箱の左半分にある白玉の数が \( n \) となる「場合の数」を,\( W( n ) \) で表そう。
箱の左半分では,白玉が \( n \) 個のとき,赤玉は \( N - n \) 個。
よって \( W( n ) \) は,白玉 \( N \) 個から \( n \) 個をとる組み合わせの数と,赤玉 \( N \) 個から \( N - n \) 個をとる組み合わせの数の積になる:
\[
W( n ) =\ _{N} C_{n} \times _{N} C_{N - n} =\ ( _{N} C_{n} )^2
\]
W( n ) は,とんでもなく大きな数になる。
「場合の数」として捉えるには,このままでは不便である。
そこで,大きな数を扱うときの常套を用いる。
即ち,対数 (桁数) で表現することにする:
\[
S( n ) =\ log\ W( n )
\]
S( n ) の表現のよいところは,これのグラフまで書けることである。
やってみよう。
\[
\begin{align}
S( n ) &=\ log\ ( _{N} C_{n} )^2 \\
&=\ 2\ log\ \frac{ N! }{ n! (N - n )! } \\
&=\ 2\ ( log\ N! - log n! - log (N - n )! ) \\
\end{align}
\]
スターリングの近似公式を用いて
\[
\begin{align}
\frac{ S( n ) }{ 2 }
&=\ ( N\ log\ N - N ) \\
&\quad - ( n\ log\ n - n ) \\
&\quad- ( (N - n )\ log\ (N - n ) - (N - n ) ) \\
\\
&=\ N\ log\ N - n\ log\ n - (N - n )\ log\ (N - n ) \\
\end{align}
\]
さらに変形して
\[
\begin{align}
\quad &=\ - n\ log\ n + n\ log\ N \\
&\quad - (N - n )\ log\ (N - n ) + (N - n )\ log\ N \\
\\
\quad &=\ ( - n )\ ( log\ n -\ log\ N ) \\
&\quad - (N - n )\ ( log\ (N - n ) - \ log\ N ) \\
\\
\quad &=\ ( - n )\ log\ \frac{ n }{ N }
- (N - n )\ \bigl( log\ ( 1 - \frac{ n }{ N } \bigr) \\
\\
\quad &=\ - N \bigl(\ \frac{ n }{ N }\ log\ \frac{ n }{ N }
+ \bigl(1 - \frac{ n }{ N } \bigr)\ log\ ( 1 - \frac{ n }{ N } \bigr) \bigr)
\end{align}
\]
ここで
\[
p( n )\ =\ \frac{ n }{ N }
\]
とおき,\( S( n ) / 2 \) を改めて \( S(n) \) と措くと,
\[
S( n ) = - N\ (\ p( n )\ log\ p( n )
+ ( 1 - p( n ) )\ log\ ( 1 - p( n )\ )
\]
こうして,\( S \) のグラフは
\[
y = x\ log\ x + ( 1 - x )\ log\ ( 1 - x )
\]
のグラフがこれの雛形になる。
\( y = x\ log\ x + ( 1 - x )\ log\ ( 1 - x ) \) のグラフは,つぎのようになる:

 \( y = x\ log\ x + ( 1 - x )\ log\ ( 1 - x ) \) のグラフ \( y = x\ log\ x + ( 1 - x )\ log\ ( 1 - x ) \) のグラフ
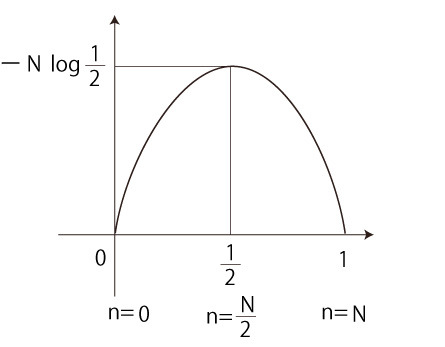
グラフは \( n = N / 2 \) を軸にしてで左右対称であり,そして \( n = 0 \) から \( n = N / 2 \) までの区間が,
「箱を降り続けていると,白赤が均等に混じった状態に至り,
その後偏った分布に戻るということは無い」
に対応している。
そこで,つぎを \( S \) のグラフにする:
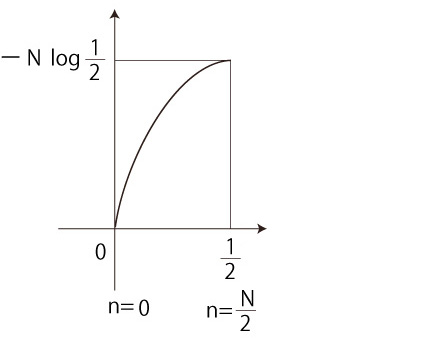
白玉の数nは,<乱雑さ>──<偏り最大>から<偏りが無い (均質)> まで──の表現である。
そして \( S \) は,乱雑さn に,n を現す<球の状態>の数 (それの桁数) を対応させる関数である。
よってこのグラフの軸の呼び方は:
|

 \( y = x\ log\ x + ( 1 - x )\ log\ ( 1 - x ) \) のグラフ
\( y = x\ log\ x + ( 1 - x )\ log\ ( 1 - x ) \) のグラフ

