Up 「物体の温度」の定義 作成: 2023-09-17
更新: 2025-02-17

    物体を，集合 \( X \) の要素の分布と考える。
    各分布 \( s \) は，各要素にスピンを対応させる関数 \( s \) である。

    「各要素にスピンを対応させる」には，＜場合の数＞が対応している。
    要素の数は多く，スピンは一般に多次元でありかつ各次元で多値である。
    よって，＜場合の数＞は途方もなく大きいものになる。

    分布 \( s \) に対し，これの＜場合の数＞の自然対数を \( s \) のエントロピーと呼び， \( e( s ) \) で表す。


    物体は「無常」である。
    この「無常」を，分布の時間的変化 (「流れ」) として考える。

    集合 \( X \) の要素の分布全体の集合を，\( D \) とする。
    時刻を１つ，時刻０として固定する。
    時間を１つ，時間の単位 \( u \) として固定する。
    流れは，関数
      \[ f : \mathbb{R} \longrightarrow D \]
    として，つぎのように定義される：
      \( x \in \mathbb{R} \) に対し \( f( x ) \) は，時間０からの経過時間が「\( u \) の \( x \) 倍」のときの分布


    流れ \( f \) は，つぎの関数 \( f_e \) を導く：
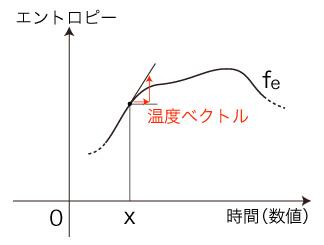
      \[ f_e = e \circ f : \mathbb{R} \longrightarrow \mathbb{R} \]

    場合の数は，途方も無く大きくとも，有限である。
    よって， \( f_e \) は階段関数になる。
    しかしその段差は， \( f_e \) の最大最小の幅と比べると，きわめて小さいと見られる。
    そこで， \( f_e \) を「滑らか」即ち「微分可能」ということにする。


    ここに至って，「物体の温度」を定義できることになる。
    即ち，「物体の温度」を「分布 \( f( x ) \) の温度 \( T( x ) \)」として，つぎのように定義する：
        \[ T( x ) = \left| \frac{ d f_e ( x ) }{ d x } \ \right| \]

    ここで定義した温度は，１次元実ベクトル (正負の実数) の絶対値であり，０以上の正値である。 ──この「温度０」が, 「絶対零度」。
    そしてつぎのようになる：
    　 分布の変化がエントロピーの大きな変化になるところで，温度は高い。

    念のため：
      温度ベクトルの正負は，日常生活で使っている温度の「プラスマイナス」ではない。


    「エントロピー」に見ている意味は，「乱雑さ」である。

    物の温度は，分布の時間的変化 (流れ) から導かれた。
    そのとき，流れは「エントロピーの流れ」に表現された。
    温度の定義は，エントロピーの変化率を温度ベクトルと定義するものである。
    これは，「乱雑さの変化速度」を温度ベクトルと定義したわけである。