- 物理法則
- 物理量 (気温，風，湿度など) の時間変化を現す式
- 各種物理量の関係を表す方程式 (状態方程式)
- 計算
- 各種物理量を時空間方向に離散化
- 格子点に初期値を措く
時間微分を含む方程式の時間発展を解く
これをループ
|
予報変数 \( \phi \) の基礎方程式を，離散化した基礎方程式で解く：
\[
\quad \frac{\partial \phi}{\partial t} = F
\ \ \longrightarrow \ \ \
\phi_{t + \Delta t} = \phi_t + F_t \Delta t
\]
|
- 基礎方程式
気象庁『数値予報解説資料集』, p.38 から引用：
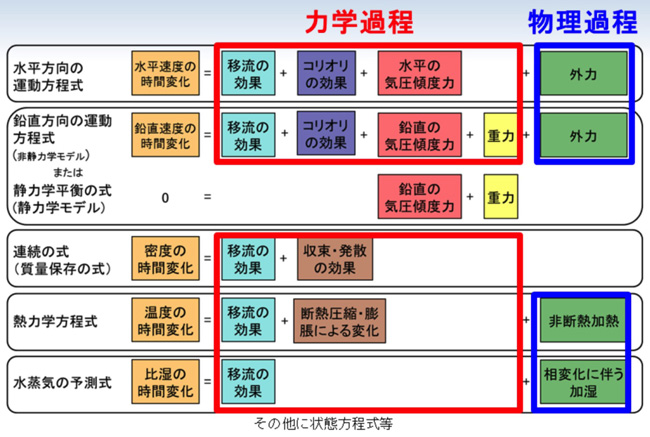
- 運動方程式は，大気の流れ（風）を支配する方程式。
- 鉛直流は，鉛直方向の運動方程式か静力学平衡の式で求める。
静力学平衡の式は，計算量が少なくなるというメリットがある。
- 連続の式は，水の相転移を除いて、空気の質量が保存されていることを表す方程式。
- 熱力学方程式は，大気の温度変化に関する方程式。
温度の代わりに温位で表される場合もある。
- 水蒸気の予測式は，大気の水蒸気の変化に関する方程式。
- このほかにも大気の状態に関する関係式である状態方程式や大気の乱流エネルギー、
地中温度などの物理量の方程式を考える場合がある。
- 静力学平衡の仮定をする方程式系を採用した数値予報モデルを「静力学モデル」と呼び、静力学平衡の仮定をしない非静力学方程式系を採用したモデルを「非静力学モデル」と呼ぶ。
静力学モデルでは、鉛直方向の運動方程式の代わりに連続の式と水平方向の運動方程式による水平方向の風の計算結果を用いて、鉛直流が求められる。
- 物理過程のパラメタリゼーション
- 各種物理量を時空間方向に離散化
- 格子点に初期値を措く
時間微分を含む方程式の時間発展を解く
これをループ
|
数値予報モデルの計算
