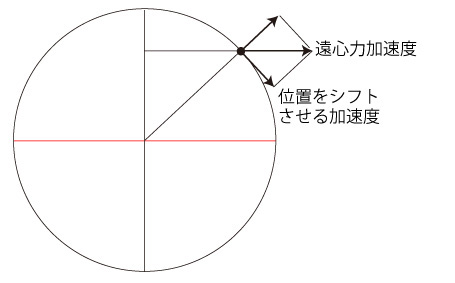
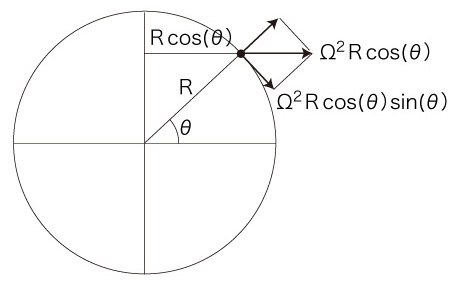
地球の半径を \( R \) m,自転の角速度を \( \Omega \) ラジアン/s とすると,緯度 \( \theta \) ラジアンにおける位置シフト加速度 \( a( \theta ) \) m/s2 は,
\[
a( \theta ) = \Omega^2\ R\ cos( \theta )\ sin( \theta )
\]
\( R, \Omega \) は,「地球1周 4万km」「1日24時間」を使って,つぎのように計算される:
\[
R = \frac{ 40000 \times 1000 }{ 2 \pi } \\
\ \\
\Omega = \frac{ 2\ \pi }{ 24 \times 60 \times 60 }
\]
よって,
\[
a( \theta ) = \Omega^2\ R\ cos( \theta )\ sin( \theta ) \\
= 2 \pi \frac{ 40000 \times 1000 }{ ( 24 \times 60 \times 60 )^2 } \ \ \ cos( \theta )\ sin( \theta ) \\
\approx 0.03368\ cos( \theta )\ sin( \theta ) \\
\]
ひじょうに小さい値である。
| 註: |
地球の自転は,地上の点の回転速度を「4万km/日 = 463m/秒」と表現すると,すさまじい速さに感じる。
一方,「回転速度 360°/日 = 0.0004°/秒」と表現すると,ひじょうにゆっくりに感じる。
どちらの感覚が当たっているかというと,後者である。
「距離/時間」表現は自転体のスケールに依存するが,「回転角度/時間」表現は自転体のスケールに依存しないからである。
|
|



