そして箱を振る。 長時間よく振ってやれば、赤玉白玉が均質に混じる。 これは，「統計的に確率の高い状態が実現される」の現象である。 （  「統計的に確率の高い状態が実現される」）
そこで，「エントロピー増大則」の事例になる。 では，この場合＜熱エネルギー → エントロピー＞関数はどう考えればよいのか。 「エントロピー」理論にあたると，「熱エネルギー」のことばは空回りしていることが見出される。 理論の中では「熱エネルギー」は形式であって，「熱」である必要はない。 （Cf. 「エントロピー弾性」） この形式に則ると，上の「直方体の箱の中で赤玉白玉が混ざる」では，＜熱エネルギー → エントロピー＞関数はつぎのように定めればよい： この＜熱エネルギー → エントロピー＞関数を，実際に求めてみよう。 (1) ｎ個の赤玉が左側にある組み合わせの数Ｗは， Ｎ! × Ｎ! /((Ｎーｎ)! × (Ｎーｎ)! × ｎ! × ｎ!)
赤玉N個からｎ個をとる組み合わせの数は，ＮＣｎ。 白玉N個から Ｎーｎ個をとる組み合わせの数は，ＮＣｎ。 よって，ｎ個の赤玉が左側にある組み合わせの数Ｗは：
＝ Ｎ! /((Ｎーｎ)! × ｎ!) × Ｎ! /((Ｎー(Ｎーｎ)! × (Ｎーｎ!) ＝ Ｎ! × Ｎ! /((Ｎーｎ)! × (Ｎーｎ)! × ｎ! × ｎ!) (2) Ｓ ＝ ーＭ ( H log H ＋ (1ーH) log(1ーH ) ) ここで，Ｍ＝２Ｎ (玉の総数)。
＝ log (Ｎ! × Ｎ! /((Ｎーｎ)! × (Ｎーｎ)! × ｎ! × ｎ!)) ＝ 2 log Ｎ! ー2 log(Ｎーｎ)! ー 2 log ｎ! スターリングの近似公式を適用して ＝ 2 (Ｎ logＮー Ｎ) ー2 ((Ｎーｎ) log(Ｎーｎ) ー (Ｎーｎ)) ー ２(ｎlog ｎーｎ) ＝ 2 (Ｎ logＮー Ｎ ー (Ｎーｎ) log(Ｎーｎ) ＋ (Ｎーｎ) ー ｎlog ｎ＋ｎ) ＝ 2 (Ｎ logＮ ー (Ｎーｎ) log(Ｎーｎ) ー ｎlog ｎ ) ＝ 2 ( ーｎ( log ｎー log Ｎ ) ー (Nーｎ) ( log(Nーｎ) ー log Ｎ ) ＝ ー2N ( ｎ/N log ｎ/Ｎ ＋ (1ーｎ/N) log (1ーｎ/Ｎ) ) ＝ ーＭ ( H log H ＋ (1ーH) log(1ーH ) ) 0 ≤ H ≤ 1 ( ⇐ H ＝ ｎ/Ｎ ) に留意して，Ｓ ＝ ーＭ ( H log H ＋ (1ーH) log(1ーH ) ) のグラフを描く。 つぎが ｙ＝ｘ log x ＋ (1ーｘ) log (1ーｘ) のグラフであった ( エントロピー関数)：
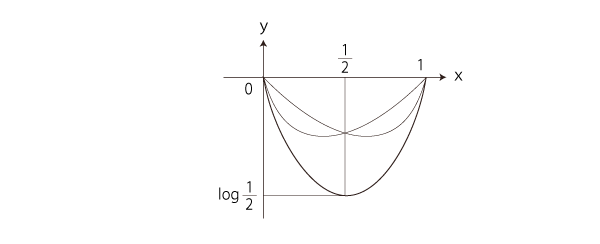
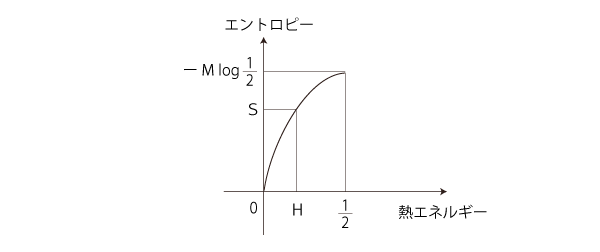
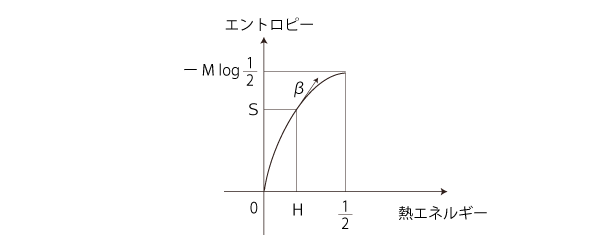
このグラフから，温度βと熱エネルギーＨの対応グラフも読み取れる：
βの増大と Hの減少が対応 β＝ ∞ と H ＝ ０ が対応 実際，関数：β├→ H の式は，Ｈ ＝ 1 / (ｅεβ ＋１ ) ── ここで，ε ＝ 1/Ｍ。
＝ d(ーＭ (Ｈ log Ｈ + (1ーＨ) log (1ーＨ) )/dＨ ＝ ーＭ ( ( log Ｈ＋ Ｈ・1/Ｈ ) ＋ ( (ー1) log (1ーＨ) ＋ (1ーＨ)・(ー1/ (1ーＨ)）) ＝ ーＭ ( log Ｈ＋ 1 ー log (1ーＨ) ー1 ) ＝ ーＭ log Ｈ/(1ーＨ) ⇐⇒ Ｈ/(1ーＨ) ＝ ｅーεβ ⇐⇒ Ｈ ＝ (1ーＨ) ｅーεβ ⇐⇒ Ｈ (１＋ ｅーεβ ) ＝ ｅーεβ ⇐⇒ Ｈ ＝ ｅーεβ / (１＋ ｅーεβ ) ＝ 1 / (ｅεβ ＋１ ) |