これは,統辞論 (syntax) と意味論 (semantics) の併行構築になる。 この内容は,基礎概念 (無定義) と公理の設定である。 「<種・必然>の力学」の理論構築では,つぎの二つが基礎概念 (無定義) になる: 系は,誕生し,生き,そして死ぬ。 系の<誕生>は,<エントロピーゼロから開始>である。 系の<生きる>──ここでは<種・必然を生きる>──は,<エントロピー増大にかなうエネルギーシフトを,その都度行う>である。 系の<死>は,<エントロピーのこれ以上の増大は,かなわない>である。 系の<生きる>──<向エントロピー増大のエネルギーシフトを,その都度行う>──を,シフトしたエネルギーと実現したエントロピーの関数と見る:
そして,エントロピー増大にシフトのエネルギーxがf'(x) =0 を満たすところで,<死>となる。 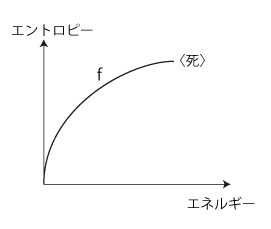
「エネルギー不変」と定めている系のそのエネルギーを,統計力学に倣って,Eで表す。 Eは,系の各ステージで,エントロピー増大に既にシフトされたエネルギーと未だシフトされていないエネルギーの和になる。 統計力学に倣い,未だシフトされていないエネルギーを「自由エネルギー」,既にシフトされたエネルギーを「熱エネルギー」と呼ぶ。 「自由エネルギー」の名の趣意は,「本来,用途自由」である。 「熱エネルギー」の名の趣意は,以下に示すように,「温度」と係わるからである。
定義から,系のエネルギーE,自由エネルギーF,熱エネルギーH,エントロピーS,関数fは,つぎの関係になる:
f(H) = S 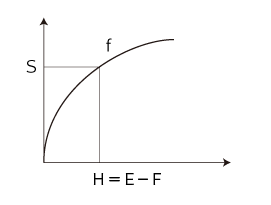
関係「f(H) = S」は,つぎのようにも書ける: 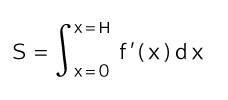
ここで,統計力学/熱力学の記号法に近づけるために,f′ をβと書く。 そして,「温度」の語を,つぎのように導入する:
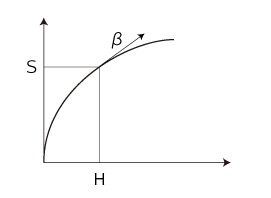
特に,系の<死>は,系の温度がゼロになるときである。 なお,βが定値関数 β(H) ≡ βであれば,
|
 「死に損なう」
「死に損なう」