二量の間の比例関係(関数)fからは,つぎのように「測定値の対応」として,数の対応が導かれます。そして,この数の対応は「一定数倍」になります。──実際,f(u) を v で測った数値 a が,その定数になります。
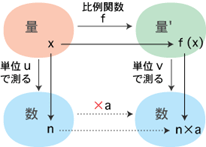
特に,定数aは,uとvに依存します (単位u, vを変えると,aの値も変わります)。
aは「uとvに関するfの表現数」と呼ぶべきものですが,「比例定数」がこれの伝統的な言い回しです。
どうして「一定数倍」になるのか,確かめるとしましょう。
量に対する数の倍作用を x で表すことにします。
「f(u) を v で測った値が a」とは,f(u) = v x a ということです。
また,x を u で測った値が n であるとは, x = u x n ということです。 このとき, f(x) を v で測った値が n × a であること,すなわちf(x) = v x (n×a) が,つぎのように導かれます:
| f(x)
|
|
| =f(ux n)
| (x = u x n)
|
| =f(u) x n
| (f が比例関数であることの条件)
|
| =(v x a) x n
| (f(u) = v x a)
|
| =v x (a×n)
| (数の積の定義)
|
| =v x (n×a)
|
|
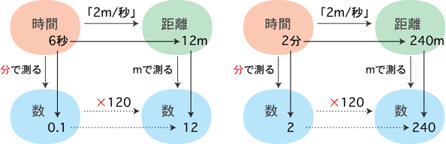
例: 比例関数「2m/秒」では,
(1) 秒とmに対する比例定数は 2:

比例定数は,小学算数ではつぎのような場面に現れています。
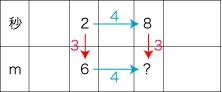
ある速さの<時間-距離の対応表>の問題:
| (1) | 比例の意味の「一方が2, 3, ‥‥倍なら他方も2, 3, ‥‥倍」を適用すれば,?=6×4。 |
| (2) | 「測定値の対応は一定数倍」を適用すれば,?=8×3。 |
|