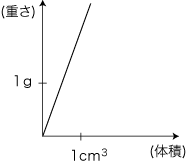
ここでは,体積(量)と長さ(量)の同型,重さ(量)と長さ(量)の同型が,暗黙に使われている。 すなわち,「1cm3」を任意に目盛ったとき,「2cm3」は,《原点から目盛り「2cm3」までの距離が,原点から目盛り「1cm3」までの距離の2倍になる》ように,「0.5cm3」は,《原点から目盛り「0.5cm3」までの距離が,原点から目盛り「1cm3」までの距離の0.5倍になる》ように,それぞれ目盛るわけである。 ──重さも同様。 さらに,わたしたちはアタリマエのように,「y=ax」の<数-数>対応をグラフにかく: 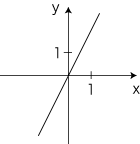
このとき,2量の比例関係から導いた数値の対応「y=ax」は,グラフにすると原点を通る直線になる。 ──《一方の<原点からの距離>の2倍,3倍,‥‥に,他方の<原点からの距離>の2倍,3倍,‥‥が応ずる》ように点をプロットすれば,それは一本の直線の上にのるわけである。(証明には,三角形の相似を使えばよい。) |