ここでは，つぎのことを調べる：
「＜地図を接ぐ＞において，曲線座標はどのよう変化していくか」
\( \phi_P\) の上で，ベクトル \( {\bf A} \) を \( P\) から \( P'\) に平行移動する：
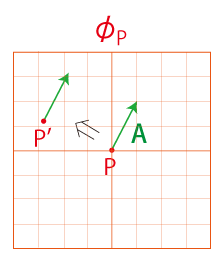
\( \phi_{P'}\) に \( \phi_P\) を読み込む：
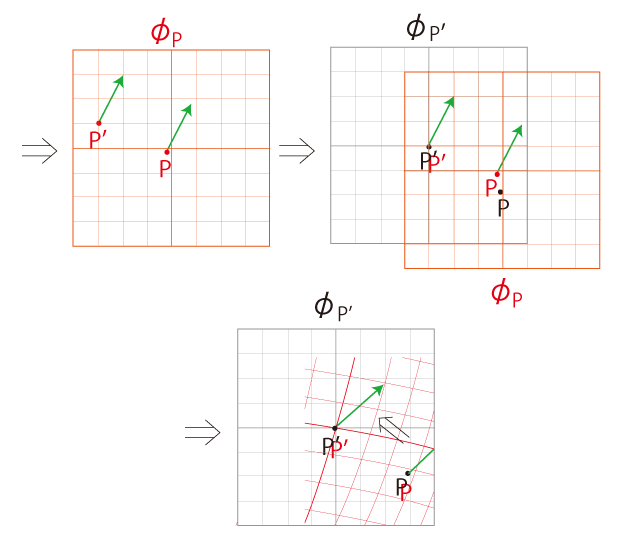
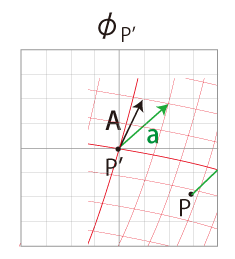
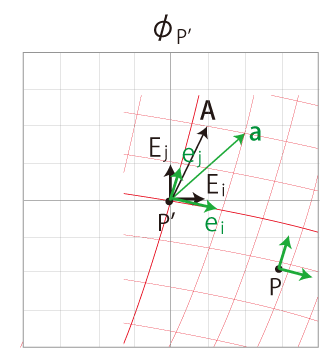
この平行移動を連続の相で見る。
即ち，\( \phi_{P'}\) の \(x^i\) 座標の基底 \( {\bf e}\) を
\[
{\bf e}({\bf x}) = \{ {\bf e}_1({\bf x}), \,\cdots ,\, {\bf e}_n({\bf x}) \}
\]
と見る。
ベクトル \({\bf a}\) を \({\bf a}({\bf x})\) と見る。
そして，\({\bf a}({\bf x})\) を，\(d{\bf x}\) だけ平行移動する。
その移動先の点 \( P''\) の地図 \( \phi_{P''}\) を開いて，\( \phi_{P'}\) を読み込む。
\(x^i\) 座標の基底を
\[
{\bf e}({\bf x}+ d{\bf x}) = \{ {\bf e}_1({\bf x}+ d{\bf x}), \,\cdots ,\, {\bf e}_n({\bf x}+ d{\bf x}) \}
\]
と見る。
そして，\({\bf a}({\bf x})\) の像を，\({\bf a}({\bf x}+ d{\bf x})\) と見る。
この設定で，「\(d{\bf x}\) に対する \({\bf a}({\bf x})\) の座標の変化」を考える。
「\(d{\bf x}\) に対する \({\bf a}({\bf x})\) の座標の変化」は，つぎのものを考える：
\[
da_i({\bf x}) = a_i({\bf x}+ d{\bf x}) - a_i({\bf x})
\\ \qquad a_i({\bf x}) = {\bf a}({\bf x}) \cdot {\bf e}_i({\bf x})
\\ \qquad a_i({\bf x}+ d{\bf x}) = {\bf a}({\bf x}) \cdot {\bf e}_i({\bf x}+ d{\bf x})
\\ \qquad \qquad \qquad ( i = 1, \cdots, n )
\]
Cf. \( {\bf a}({\bf x}+ d{\bf x}) \cdot {\bf e}_i({\bf x}+ d{\bf x}) = {\bf a}({\bf x}) \cdot {\bf e}_i({\bf x}) \)
ここで，座標の表記が添字を下付けにした「\(a_i\)」なのは, 「共変座標」だからである。
(  「共変座標」)
\( da_i({\bf x}) \) を計算する：
\[
\begin{align*}
d a_i({\bf x})
&= {\bf a}({\bf x}) \cdot {\bf e}_i({\bf x}+ d{\bf x}) - a_i({\bf x})
\\ &= {\bf a}({\bf x}) \cdot {\bf e}_i({\bf x}+ d{\bf x}) - {\bf a}({\bf x}) \cdot {\bf e}_i({\bf x})
\\ &= {\bf a}({\bf x}) \cdot \left( {\bf e}_i({\bf x}+ d{\bf x}) - {\bf e}_i({\bf x}) \right)
\\ &= {\bf a}({\bf x}) \cdot d{\bf e}_i({\bf x})
\\ &= {\bf a}({\bf x}) \cdot \left( \sum_m \sum_j \Gamma^j_{im} {\bf e}_j({\bf x}) \ dX^m \right)
\\ &= \sum_m \sum_j \Gamma^j_{im} \left( {\bf a}({\bf x}) \cdot {\bf e}_j({\bf x}) \right) dX^m
\\ &= \sum_m \sum_j \Gamma^j_{im}\, a_j({\bf x})\ dX^m
\end{align*}
\]
( 「基底の接続」)
まとめ
\[
a_i({\bf x}+ d{\bf x})
= a_i({\bf x})
+ \sum_m \sum_j \Gamma^j_{im}\, a_j({\bf x})\ dX^m
\]
|