多種多様であることは,重要である。 多種多様は,集まったときに,ほどよいバランスをつくる。 このバランスが,公教育としての数学教育を極端へと偏らせないことに効いている。 しかしこの「多種多様」は,学生指導では問題になる。 そこでは,たまたま,ある一つの<主観>が学生に対する。 数学教育の入門者である学生は,教員の<主観>に免疫をもたない。 すなわち,学生は,教員の<主観>に対し適切な距離をとるということを知らない,したがって当然,適切な距離をとれない。 人は,自分の<主観>を疑うようにはできていない。 ──小学生でも,自分はいっぱしの存在だと思っている。 教員は,自分の<主観>をよいものであると思っている。 そして,このよいものを学生に分け与えようとする。 教員は,この危うさを認識して,学生に対し「わたしを信じてはならない。」のようなエクスキューズを入れるかも知れない。 しかしこれは,アリバイづくり以上の意味をもたない。 「わたしを信じてはならない。」を言って終わるのではなく,自分を信じさせない方法をいろいろと示すところまで,もって行かねばならない。 「自分を信じさせない方法をいろいろと示す」とは,多様な<主観>の存在──特に,自分と正反対の<主観>の存在──を具体的に教えるということである。 そこで,数学教育担当教員の<主観>の布置を,問題に立てるとしよう。 数学教育の<主観>を定位する伝統的なやり方に,「数学を教える」と「数学で教える」の2分法がある。 この場合,「生活単元学習」は「数学で教える」の極にある。 「問題解決ストラティジー」で理論をつくっている「問題解決学習」も,「数学で教える」の極に近い。 「数学的な考え」は,「数学を教える」と「数学で教える」の中間点から両方向に伸びる感じになる。 1970年代の「数学教育の現代化」は,「数学を教える」の極にある。 これにさらに,合理主義/科学主義とプラグマティズムの2極構造を,追加してみる。 「プラグマティズム」は,つぎの立場である:
「授業は<要素の組み上げ>として理解されるべき」的なアプローチをしているのは,合理主義/科学主義。 これに対し,「授業は複雑系であり,よって経験的に理解されるのみ」的なアプローチをしているのが,プラグマティズム。 「よい授業」の定式化を課題にして授業分析へと進むのは,合理主義/科学主義。 そしてプラグマティズムは,このやり方をつぎのように批判するものになる:
こうして,数学教育担当教員の<主観>を定位する座標平面がつぎのように得られる: 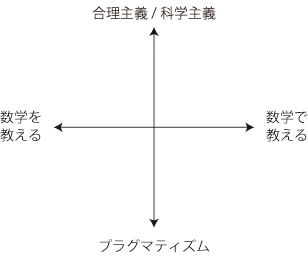
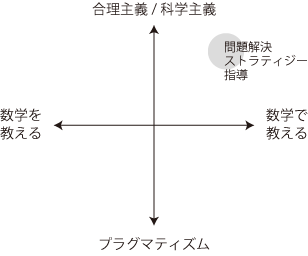
「数学教育学」のことばは,「数学」と「教育学」を合わせたものになっている。 そして,数学教育担当教員にも,数学をベースにしてきた者と教育学をベースにしてきた者の2タイプがある:
数学をベースにしてきた者は,数学から学校数学を見る。そしてそのギャップをどのように考えるべきか,最終的に授業はどうつくられるべきか,というふうに考えを進める。授業のゴールは,教えるべきと定めた数学が確かに教えられることである。 特に,「数学を教える」になる。 教育学をベースにしてきた者は,学校数学 (現前の教科書や学習指導要領) からスタートする。──学校数学の内容は,数学ベースの者のようには,批判の対象にならない。 そして,この授業で目指すものを何にするか,どのような授業にしたらよいか,というふうに考えを進める。 特に,「数学で教える」になるのが普通である。 数学教育担当教員は,自分の<主観>が上の座標平面の中のどの辺りに位置するかを押さえ,さらに学生に対して「自分の指導教員の位置」を意識するよう促さねばならない。 繰り返すが,学生は教員の<主観>に対し適切な距離をとるということを知らない。 「適切な距離のとり方」は,教員が学生に対し最初に指導すべき内容の一つである。 ちなみにわたしは,つぎの位置に居るつもりでいる: 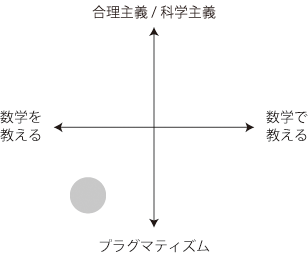
|
 学校数学の<役に立つ/立たない>とは?
学校数学の<役に立つ/立たない>とは?