Up | English 学校数学の関数の「ｘ, ｙ」の解釈  

「入出力マシン」の要素
変数と定数


    学校数学では，伝統的に「変数ｘ, ｙ」を使った関数表現を使っている。
    「変数 (variable)」とは何か？
    変わる数？
    そんなものは，数学にはない。
    数学が「対象」とするものには，それ自体が生き物のように変わるものはない。

    数学は，それ自体が生き物のように変わるものを，対象にしない。
    なぜなら，「変わるが，依然同一である」ような対象を考えることでロジックをめんどうにすることには，メリットがないからだ。

    関数は，「変化」の表現にも使うが，その表現の中には「自ら変化するもの」は存在しない。


    「変数 x, y」とは，それぞれ，ｘと名付けられた容器，ｙと名付けられた容器のことである。
    ｘにはいろいろな対象 (ただし，定義域にあるもの) を入れることができる。そして，ｘに入る対象に応じてｙにいろいろな対象が入る。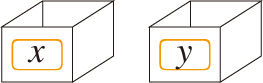


    特に，ここには「自ら変化するもの」は存在しない。


    さて，変数ｘ, ｙを使った関数表現は，どんな意味なのか？
    答： 例えば，「関数ｙ＝２ｘ」は，つぎの意味である：

      容器ｘの中に入れた数の２倍の数を，容器ｙの中に入れる働き (function)

    一方，この関数を「入出力マシン」として表現すれば，つぎのようになる：

      入力された数の２倍の数を出力する働き (function)

    この入出力マシンを図と式 (記号列) で表現するならば，つぎのような，働きの名前「ｆ」と入力容器の名前「ｘ」を使うものになる (「２ｘ」は「容器ｘに入っている数の２倍の数」の意味)：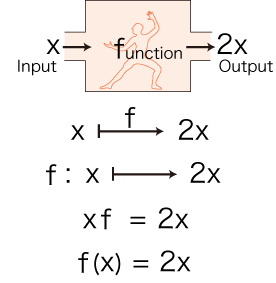



    この入出力マシンに「変数ｙ」も書き加えるならば，つぎの解釈になる：



    1. モノが，「入力」として，「ｘ」という名の容器に入れられる。
    2. 「ｆ」という名の「働き」が，「ｘ」の中にあるモノを取り出し，加工し，結果を「ｙ」という名の容器に入れる。
    3. 「ｙ」の中にあるモノが，「出力」として取り出される。

    そして，式 (記号列) 表現はつぎのようになる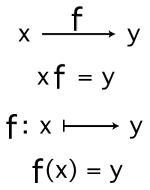：