- 定義域
- 「定義域」が関数の要素になることは，「機械」を考えるとよくわかります。
「機械」では，
の概念が決定的なものになっています。
実際，入力にならないものを入力することは，単に無効であったり，あるいは機械を壊してしまうことになるからです。
| 例 : |
車を動かすための入力は，決まっている。
動かそうとして「動け！」と叫んでも，車は動かない。
動かそうとして車のキーの穴にガムを詰め込んでも，車は動かない。むしろ壊してしまうことになる。
|
- 関数の定義域は，
f : x 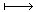 x2 | __ | ( -2 < x < 3 )
|
のように，「変数 x の条件」の形で示すのが一般的です。
- 例：
- つぎの関数は，実際，指定した定義域外の要素を入力として受け付けません：
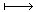| f : x 1/x | __ | ( x ≠0 )
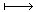| | f : x log(x) | __ | ( x > 0 )
|
- つぎの関数は，指定した定義域外の要素を入力として受け付けることができますが，ある目的から入力を制限していることになります：
| f : x 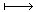x2 | __ | ( -2 < x < 3 )
|
- 値域
- 「値域」が関数の要素になることは，やはり「機械」を考えるとよくわかります。
「機械」では，
「この機械がすること」
の概念が最も肝心なものになります。
これは「出力のすべて」ですが，これが「値域」の概念に対応しています。
- 「一意対応」としての「関数」の形式化では，値域の示し方に任意性が出てきます。
すなわち，関数 f の像を含む集合は，いずれも f の値域と指定できてしまいます。
D: 定義域，V: 値域
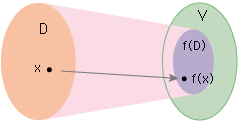
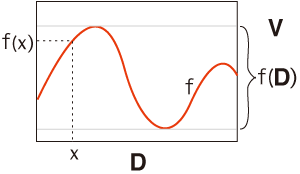
そこでこの場合，値域の表現は，
「関数 f の情報として値域をどのように示すのが適切か」
という考えのもとで，実践的に出てくることになります。
| 註 : |
ただし，「関数の像」の意味で「値域」の語を用いる立場もあります。
( 一意対応)
|
|