 ２次元の「回転・倍」は，３次元で考えている！)
これとまったく同じことが，３次元ベクトル空間の変換としての「回転・倍」についても言えます。 ３次元ベクトルに対する「回転・倍」の作用は，３次元ベクトル空間の変換 f として考えるものになります：
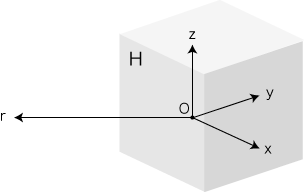
v を (1, 0, 0 ) とするように x-y-z 座標をとる。 f は，f(v) ＝ ( ax, ay, az ) で決まる。 「一つのベクトルの移動先が決まれば，すべてのベクトルの移動先が決まる」ということです。 （これは，「作用」が「数」に昇格するための基本要件です。) ここで，「v を (1, 0, 0 ) とするように x-y-z 座標をとる」に注意しましょう。 「任意のベクトル v に対し，これを (1, 0, 0 ) とする x-y-z 座標」が一意に決まらないと，「f は，f(v) ＝ ( ax, ay, az ) で決まる」のようにできません。 x 軸は一意に決まります。 しかし，この x 軸に対する y, z 軸が，一意に決まりません。 ｘ軸に対し y, z 軸が一意的に決まるようにはできないでしょうか？ ３次元ベクトル空間を４次元ベクトル空間の中に３次元超平面として埋め込めば，これができます： ２次元ベクトル空間は，３次元ベクトル空間につぎのように埋め込まれました： これとまったく同じに，３次元ベクトル空間を４次元ベクトル空間に埋め込みます： |
がある」ようにとるとき，座標が ( 0, x, y ) の形のベクトル 
全体が，q に直交する２次元超平面になる。