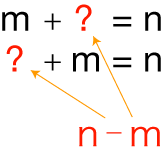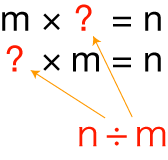数の和 (記号「+」の用い方) と積 (記号「×」の用い方) が,つぎのように定義されました:


この和・積に対し,加法,乗法,差,商が,つぎのように定義されます:
「加法」
数の対(m,n)に m + n を対応させる関数を,「加法」と呼ぶ。

「乗法」
数の対(m,n)に m × n を対応させる関数を,「乗法」と呼ぶ。

「差」(記号「ー」の使い方)
m,n に対し, m + ? = n となる数 ? を対象化し,これを「n − m」と表わす。
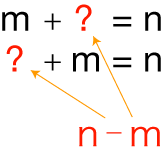
| 注意 : |
「n − m」は,存在しないこともあり得ます。
(「対象化する」と「それが実際に存在する」は,別のことです。)
|
| 例 : |
自然数では,「2 − 3」(「3 とたして 2 になるもの」) は存在しません。
しかし,「2 − 3」の対象化を対象化することはできます。
現に,「自然数では 2 − 3 は存在しない」の言いまわしに,「2 − 3」が対象化されています。
強調:「対象化する」と「それが実際に存在する」は,別のことです。
|
「商」(記号「÷」の使い方)
m,n に対し, m × ? = n となる数 ? を対象化し,これを「n ÷ m」と表わす。
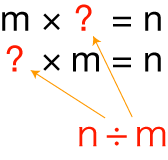
| 注意 : |
「n ÷ m」は,存在しないこともあり得ます。
(「対象化する」と「それが実際に存在する」は,別のことです。)
|
| 例: |
自然数では,「2 ÷ 3」(「3 とかけて 2 になるもの」) は存在しません。
しかし,「2 ÷ 3」を対象化することはできます。
現に,「自然数では 2 ÷ 3 は存在しない」の言いまわしに,「2 ÷ 3」が対象化されています。
強調:「対象化する」と「それが実際に存在する」は,別のことです。
|
|
 算法──内算法(演算)と外算法(作用)
算法──内算法(演算)と外算法(作用)




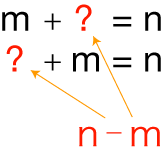
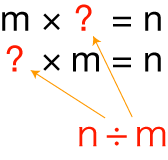
 算法──内算法(演算)と外算法(作用)
算法──内算法(演算)と外算法(作用)