この「直線上方向自由な向きと大きさをもつ量」の考えを延長すると,「平面上方向自由な向きと大きさをもつ量」(高校数学に出てくる「平面上のベクトル」) になります: 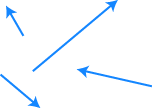
すなわち,つぎのようになります: 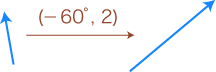
(数学では,時計回りがマイナスで,逆がプラス)
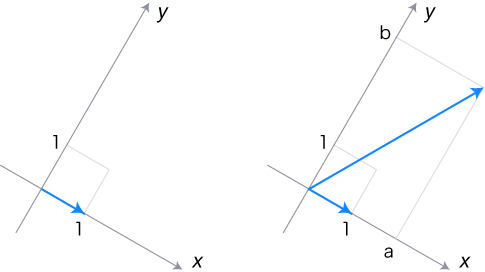
──「正負の数」のしくみの単純な拡張であることを,確認してください。 しかし,複素数をこのように説明すると,「高校で習った複素数はこんなんじゃない。高校では a + biみたいに習った。」のことばが返ってきそうです。 表現「a + bi」のしくみを,説明しましょう。 ここに (θ, d) と表現されている比があります: 
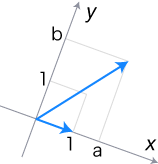
( y軸の正方向は「x軸の +90゜回転」のルールで決められる)
練習として,具体的な例でやってみましょう: 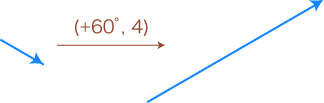
高校で複素数を習ったひとは,実はこの2つの表現とその換算法も学習しています。 (しかしほとんどのひとは,これの意味を知らないで/意識しないで過ごしてきています。) 複素数zの二つの表現a + biと (θ, d) に対し,zの偏角と呼ばれ arg(z) と表記されたのがθで,zの絶対値と呼ばれ |z| と表記されたのがdです。 そして以下が,換算法です: 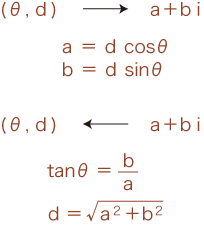 |