この合成で (vx, vy, vz) が移る先 (wx, wy, wz) は,つぎの計算で求められます:
× (vx i + vy j +vz k) × 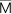 ((1, 0, 0), π) ) × ((1, 0, 0), π) ) × 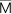 ((0, 1, 0), π) ) ((0, 1, 0), π) )
= wx i + wy j +wz k このとき,
= (cos(π/2) + (0 × sin(π/2)) i + (1 × sin(π/2)) j + (0 × sin(π/2)) k) × (cos(π/2) + (1 × sin(π/2)) i + (0 × sin(π/2)) j + (0 × sin(π/2)) k) = j × i = ーk
qx sin(θ/2) = 0 qy sin(θ/2) = 0 qz sin(θ/2) = ー1 cos(θ/2) = 0 より θ/2 = ±π/2,さらに
または sin(θ/2) = ー1, qx = 0, qy = 0, qz = 1 地球儀などを使って,この回転が求めるものになっていることを実際に確認してみてください。 例2. つぎの2つの回転を合成します: そして,この結果がつぎの回転であるとしましょう: この合成で (vx, vy, vz) が移る先 (wx, wy, wz) は,つぎの計算で求められます:
× (vx i + vy j +vz k) × 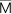 ((1, 0, 0), π/3) ) × ((1, 0, 0), π/3) ) × 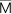 ((0, 1/√2, 1/√2), π/3) ) ((0, 1/√2, 1/√2), π/3) )
= wx i + wy j +wz k このとき,
= (cos(π/6) + (0 × sin(π/6)) i + (1/√2 × sin(π/6)) j + (1/√2 × sin(π/6)) k) × (cos(π/6) + (1 × sin(π/6)) i + (0 × sin(π/6)) j + (0 × sin(π/6)) k) = (√3/2 + √2/4 j + √2/4 k) × (√3/2 + 1/2 i)
qx sin(θ/2) = √3/4 qy sin(θ/2) = (√6 + √2)/8 qz sin(θ/2) = (√6 ー√2)/8 cos(θ/2) = 3/4 より,
または sin(θ/2) = ー√7/4, qx = ー√3/√7, qy = ー(√6 + √2)/(2√7), qz =(√6 ー√2)/(2√7) この数値は,つぎの関係を確かに満たしています:
|