2つの小数の小数点以下の桁数を足す。 この数が小数点以下の桁数になるように,かけ算で出した数に小数点をつける。 この計算法の理由は,つぎのようになります。──例として 1.23 × 0.4 を考えます: 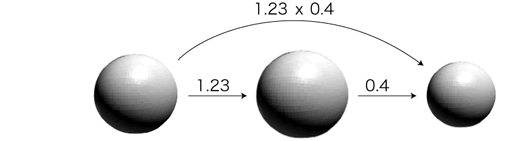
 「小数倍」の文法): 「小数倍」の文法):
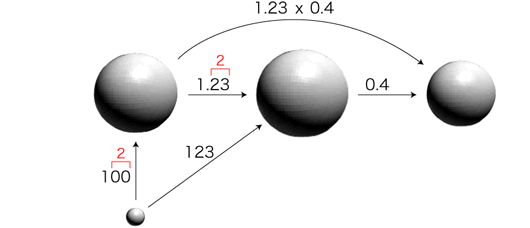
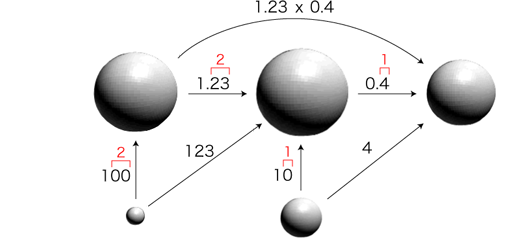
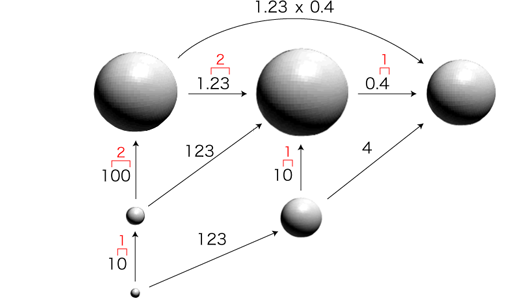
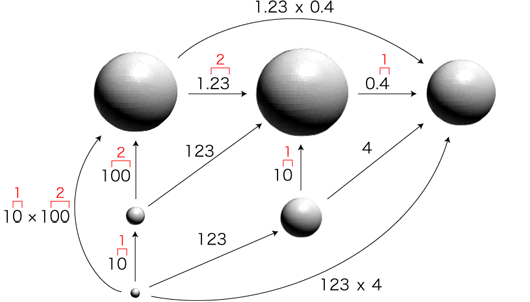
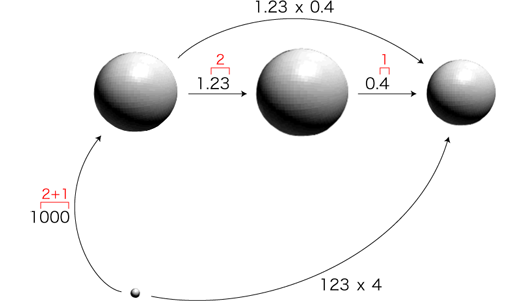
 「小数倍」の文法): 「小数倍」の文法):
このように,小数の求積計算の理由の説明は,きわめて数学的 (難解) なものになります。 よって,小学校段階ならつぎのような指導法も「あり」でしょう:
小数の積の計算法として,このやり方を覚えましょう。」 なお,「小数を分数に翻訳」と「分数の積」を既習として使うことにすれば,計算法の考え方/解釈がはるかに簡単になります:
2. 分数の積を求める(分子同士をかけ,分母同士をかける)。 3. 得られた分数を,小数に替える。 このとき,「分子同士をかける」が「整数計算」に,「分母同士をかける」が「小数点の位置の計算」に,それぞれ相当する。 |