nを十分大きい数とする。 母集団からn個の標本を抽出し,そして平均を出す。 これを何回も行う。 平均の分布は,母集団の分布とは関係なく,<平均μ,標準偏差 σ/√n の正規分布>に近づく。 →「nが大きいとき,標本抽出を1回やって,これの平均を母集団の平均だということにしてよい。」
なお、標本の分布に分散が存在しないときには、極限が正規分布と異なる場合もある。 統計学における基本定理であり、例えば世論調査における必要サンプルのサイズの算出等に用いられる。 定理 期待値 μ, 分散 σ2 の独立同分布 ("i.i.d.") 確率変数 ("r.v.") 列 X1, X2, ... に対し、 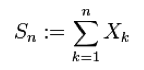
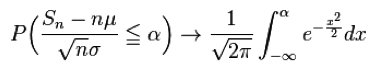
従って、n が十分大きいとき近似的に、標本平均 [Xn] と真の平均 μ との誤差 [Xn] ーμ をルートn倍したものは,平均 0, 分散 σ2/n の正規分布 N(0, σ2/n) に従う。 |