量の<リンゴの個数>,<皿の枚数>の系を ,それぞれ ( (Qリンゴ, , +), ×, (N, +, ×) ), ( (Q皿, +), ×, (N, +, ×) ) で表す。 ここで, 「リンゴ1個」と呼んでいるQリンゴの要素を,記号「個」で表す。 そこで,たとえば「リンゴ2個」は「個× 2」と表される。 同様に,「皿1枚」と呼んでいるQ皿の要素を,記号「皿」で表す。 そこで,たとえば「皿3枚」は「皿× 3」と表される。 ( (Q皿, +), ×, (N, +, ×) ) と ( (Qリンゴ, +), ×, (N, +, ×) ) の間には,比例関係 (準同型) が考えられる。 比例関係 (準同型) 全体の集合を,Hom( Q皿, Qリンゴ) で表す。 Hom( Q皿, Qリンゴ) の要素に対しては,和と数の倍作用が標準的に定義される: ( (Hom( Q皿, Qリンゴ), +), ×, (N, +, ×) ) は, ( (Qリンゴ, +), ×, (N, +, ×) ), ( (Q皿, +), ×, (N, +, ×) ) と同型な系になる。すなわち,量になる。 「密度」を量として扱うことがあるが,それはこういう数学をやっていることになる。
速さとは,時間と距離の間の比例関係のことである。これが量として扱われるときは,( (Hom( Q時間, Q距離), +), ×, (N, +, ×) ) を考えていることになる。──このときのNには,ふつう正の実数 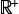 が択ばれる。 が択ばれる。
比例関係は,皿の枚数 (≠ 0) とリンゴの個数の対応ペアを一つ定めれば,それで決定される。 いま,皿に個が対応する比例関係を「個/皿」で表す。 関数F : Hom( Q皿, Qリンゴ) × Q皿 → Qリンゴ を
 x と書ける: x と書ける:

 皿 = 個 である。 皿 = 個 である。
これらの準備を経て遂に,「(個/皿 × 2)  (皿 × 3) = 個 × 6」としての「2個/皿 × 3皿 = 6個」の計算へと進むことができる。
即ち,つぎのようになる:
(皿 × 3) = 個 × 6」としての「2個/皿 × 3皿 = 6個」の計算へと進むことができる。
即ち,つぎのようになる:
 (皿 × 3)
(皿 × 3)
=F(個/皿 × 2, 皿 × 3) =(個/皿 × 2)(皿 × 3) =((個/皿 × 2)(皿)) × 3 =(((個/皿)(皿)) × 2) × 3 =個 × (2 × 3) = 個 × 6 さらに記号  を専ら使うことにすれば,つぎのようになる: を専ら使うことにすれば,つぎのようになる:
 (皿 × 3)
(皿 × 3)
=((個/皿 × 2)  (皿)) × 3 (皿)) × 3
=(((個/皿)  (皿)) × 2) × 3 (皿)) × 2) × 3
=個 × (2 × 3) = 個 × 6 |
 を択ぶことになる。
を択ぶことになる。