そこで,放射能数値の安全/危険度は,いまの時点ではつぎのモデルで考えればよいことになる:
ここでは,体内被曝の計算がこのモデルの場合どのようになるかを見ていく。 ただし,計算を考えやすくするために,半減期が8日の放射性ヨウ素のみを,放射性物質として考えることにする。 いま,<呼吸する・水を飲む・食事する>の形で,
「最初の爆発でその後が決定」のモデルでは,つぎの見方が成り立つ:
すなわち,最初に取り込んだ量がaベクレルであるとき,その時から時間x (単位:日) が経過した時点で,A1 〜 An 全部の摂取により取り込む放射性ヨウ素の量 f(x) は,つぎのようになる: 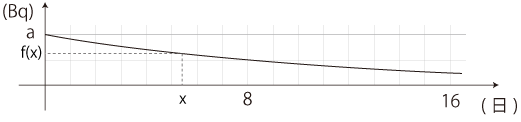
簡単のために,<呼吸する・水を飲む・食事する>を「毎日零時に一回」のことにしよう。 x日の零時に,そのときの体内蓄積量に f(x) が加わる。 そして,翌日までの間に,体内の放射性物質が<半減期>の法則で減少する。 このときの体内蓄積量の推移をグラフの手作業で求めると,つぎのようになる (赤色の部分): 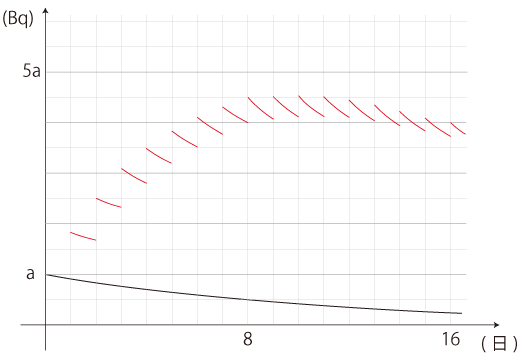
以上は「最初の爆発でその後が決定」モデルに順った場合であるが,比較のために,「放射能数値を保つ具合に放射性物質の放出が続いている」モデルではどうなるかを,示しておく──この場合は,蓄積量が単純増加する: 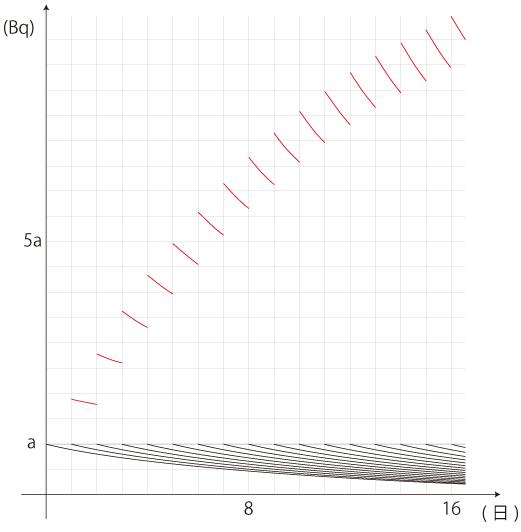
放射性セシウムのように半減期が長い場合だと,蓄積量は少なくともしばらくの期間,単純増加する。 よって,安全基準値をかなり下回る値であっても,軽んじることはできない。A1 〜 An が含有する放射性物質の量を継続的にチェックし,体内蓄積量の推移をしっかり計算していくことが必要となる。 政府・マスコミおよびこれの御用になる学者は,いまのところ,この計算を示していない。 よって,個人のつぎの行動を指して「風評被害」と呼ぶのは,当たらない:
|
 2011-04-09 時点の状況認識
2011-04-09 時点の状況認識