放射線量は,シーベルト (Sv) を単位にして表される。
そして,シーベルトの千分の一がミリシーベルト (mSv) で,さらに千分の一がマイクロシーベルト (μSv) である。
自分の被曝量 (mSv 単位相当) は,自分が生活している地域においてモニタリングされている被曝率 (μSv/時 単位相当) のデータから概算できる。
また,原発からの放射性物質の飛散傾向から,被曝量の今後の推移を予測できる。
ここでは,この概算,予測の方法を示す。
先ず,「被曝率一定」 モデルを使えるようにしよう。
これは,時間帯が「日」を越えると現実的でないモデルになるが,短い時間帯には実際的なモデルになる。
──実際,被曝率の推移は,小さな「被曝率一定」に区分した形で捉えることになる。
「被曝率一定」 モデルは,小学算数の「比例関係」の内容である。
例えば,「4μSv/時 の地点に5時間いたら,何μSvの被曝になるか?」の問題は,「4km/時 で5時間歩いたら,何km の移動になるか?」の問題と同型であり,小学生でも「(4×5) μSv」と答えられねばならないものである。
さらに,つぎの2つのグラフも,本来書けねばならない:
| |
A. <測定開始時からの経過時間>に対する<被曝率>の変化
B. <測定開始時からの経過時間>に対する<被曝量>の変化
|
「4μSv/時」の2つのグラフは,つぎのようになる:
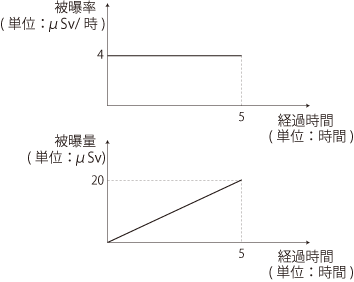
そこで,被曝率 (μSv/時 単位相当) の変化のグラフから,被曝量の累積のグラフがつぎのように導かれる (やっていることは「区分求積」):
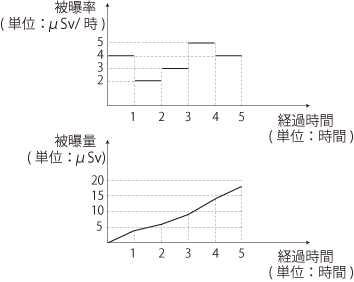
ただし,ふつうは「本日の値」のようにデータが提供されるので,「日」を時間の単位にしたつぎのようなグラフを書くことになる:
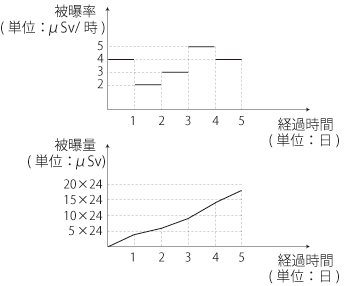
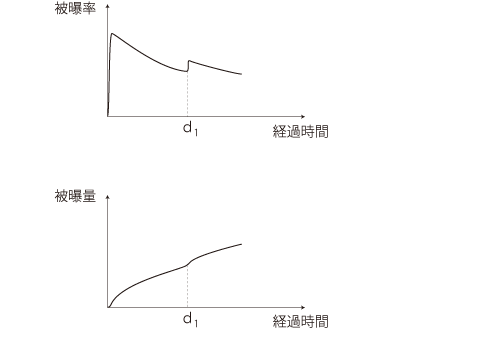
さて,原発事故発生時を測定開始時にしたときの「<測定開始時からの経過時間>に対する<被曝率>の変化」の実際は,つぎのパターンを現すものになっている:
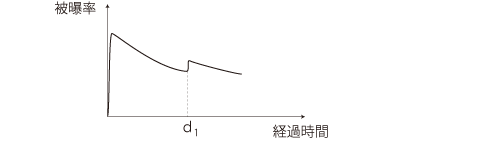
解説:
- 被曝率の最初の跳ね上がりは,地震2日後と3日後に相継いで起こった原発の水素/水蒸気爆発で大量に飛散した放射性物質に因る。
- この後被曝率の値が下がるのは,主に拡散と,放射性物質のうち半減期の短いものの総量が減少していくため。
- ただし放射性物質の量は,拡散と半減期が<減少>の要因になる一方で,原発からの新たな飛散が<増加>の要因になる。
この2つの相殺の結果が,現前の<減少傾向の鈍さ>である。
- しかも,半減期の長い放射性物質は,半減期による<減少>よりも新たな飛散による<増加>の方が勝ってしまう。
- d1 の跳ね上がりは,風下で多くの放射性物質が運ばれてくるとか,雨によって大気中に漂っている放射性物質が降ってくる場合。グラフは一つだけ書いているが,これは何度もある。 また,グラフは跳ね上がりの大きさを強調して書いているが,大嵐が原発の粉塵を巻き上げるみたいなときは顕著な跳ね上がりになるだろう。
|
この「<測定開始時からの経過時間>に対する<被曝率>の変化」のグラフから,上に述べた「区分求積」を使って,「<測定開始時からの経過時間>に対する<被曝量>の変化」の変化のグラフがつぎのように得られる──実際に手作業でやってみるとよい ( 「微積分」入門): 「微積分」入門):
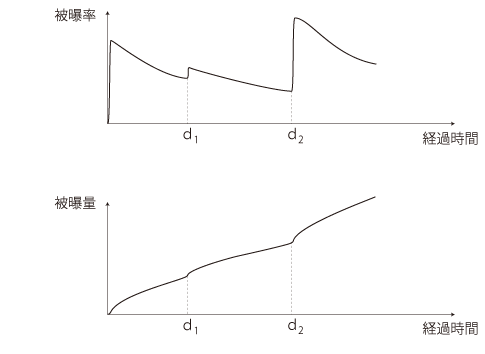
ここで,もしまた爆発が起こり,多くの放射性物質が飛散することになれば,つぎのようなグラフになる:
被曝量の安全基準は,ICRP勧告では「年間 1mSv 」である。
また,ICRP は,この度の Fukushima Nuclear Power Plant Accident (ICRP, 2011-03-21) において,「このようなときでも年間 1mSv 〜 20mSv」を説き,むやみに「安全基準」を引き上げることを牽制している。
──実際,マスコミに登場の学者のうちには,「100mSv」を安全基準のように言う者も一時いたわけである。
「安全基準」は,これをめぐる科学と政治を考慮しつつ,自分で決める他ない。
そしてこのとき,自分の被曝量がつぎのようになっていることが,「自分は安全」の定義になるわけである:
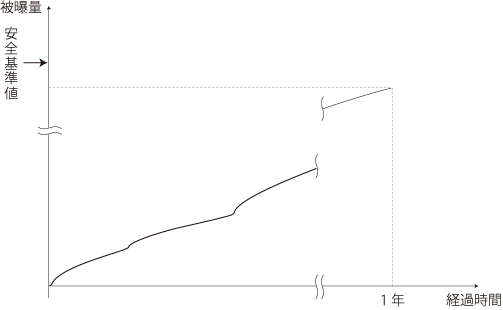
|




 「微積分」入門):
「微積分」入門):


